該示例演示了一種基于光纖布拉格光柵（FBG）的溫度傳感器，因?yàn)楣饫w折射率會(huì)隨溫度而變化，導(dǎo)致其布拉格波長(zhǎng)發(fā)生偏移，所以可以被用作溫度的測(cè)量。
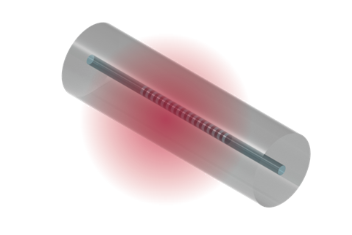
在本示例中要考慮的光纖布拉格光柵（FBG）由具有交替折射率和恒定周期性的纖芯制成。眾所周知，沿著光纖主軸的折射率變化可以在布拉格波長(zhǎng)（λ_Bragg）下引起反向傳播模式的耦合，由以下方程給出：
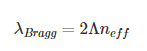
其中n_eff是布拉格波長(zhǎng)下光纖基模的有效折射率，Λ是光柵的周期。均勻的FBG在布拉格波長(zhǎng)下起到波長(zhǎng)選擇鏡的作用。在沿著光纖軸的每個(gè)折射率不連續(xù)處，都會(huì)發(fā)生微弱的菲涅耳反射。當(dāng)來(lái)自界面的所有反射累積時(shí)，光柵在布拉格波長(zhǎng)周圍產(chǎn)生一個(gè)明顯由旁瓣包圍的反射帶。
上述方程可以擴(kuò)展為包括溫度（T）對(duì)折射率的影響，從而包括布拉格波長(zhǎng)：
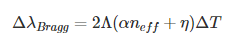
其中，α和η分別代表光柵材料的熱膨脹系數(shù)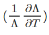
和熱光系數(shù)
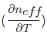。溫度的變化(ΔT)導(dǎo)致纖芯和包層的折射率變化，變化量由η值決定(通常為
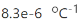)，***終導(dǎo)致布拉格波長(zhǎng)偏移。光纖的膨脹也會(huì)導(dǎo)致布拉格波長(zhǎng)的偏移。然而，我們通常會(huì)忽略后一種效應(yīng)，因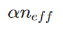?yàn)?img data-imageid="0" src="https://0.rc.xiniu.com/g5/M00/04/C0/CgAGbGVmnQ2AAHrlAAAFFMy4SjU514.png" style="max-width:100%;" alt="Lumerical光纖布拉格光柵溫度傳感器的仿真模擬" title="Lumerical光纖布拉格光柵溫度傳感器的仿真模擬"/>（通常為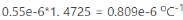
）是小于η的一個(gè)數(shù)量級(jí)。我們采用了η的二階依賴性，因?yàn)樗呀?jīng)被證明比線性模型更準(zhǔn)確，尤其是在400℃以上的溫度下。
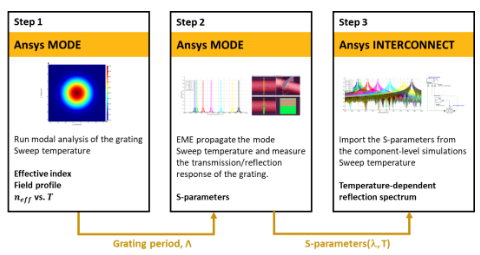
步驟1:FDE-計(jì)算光柵所需的周期和溫度相關(guān)有效折射率
我們首先使用FDE求解器獲得目標(biāo)波長(zhǎng)下光柵的有效折射率，并計(jì)算光柵的所需周期(Λ)。我們計(jì)算高折射率區(qū)域和低折射率區(qū)域的，并將其的平均值作為設(shè)計(jì)的起點(diǎn)。
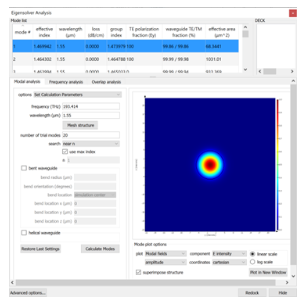
此案例中光纖由n=1.4725/1.4728（L/H）和R=4.8μm的纖芯和n=1.466和R=62μm的包層組成。使用腳本添加 FDE求解器，并在室溫下為光柵中的兩個(gè)不同位置（高折射率區(qū)域和低折射率區(qū)域）運(yùn)行模擬。有效折射率的平均值用于表示光柵的總折射率，并用于估計(jì)所需的光柵周期。本例中所考慮的基模的場(chǎng)分布如下所示。正如預(yù)期的那樣，該模式被很好地限制在光纖的核心區(qū)域。
步驟2:EME-計(jì)算光柵的溫度相關(guān)透射/反射響應(yīng)
我們分析了光柵在多個(gè)周期內(nèi)的透射/反射值，模擬區(qū)域中只包括光柵的單個(gè)周期，但通過(guò)使用“周期性”和“波長(zhǎng)掃描”特征可以獲得長(zhǎng)光柵的寬帶響應(yīng)。然后，我們掃描溫度，并將傳輸/反射響應(yīng)導(dǎo)出為S參數(shù)，S參數(shù)可用于隨后的電路模擬。
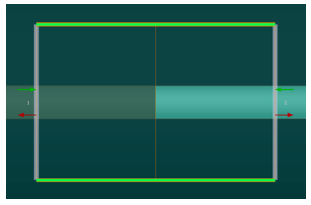
根據(jù)上一步計(jì)算的周期將自動(dòng)用于“模型”參數(shù)。使用腳本運(yùn)行EME求解器并計(jì)算布拉格光柵的S參數(shù)。我們?cè)谀M區(qū)域中有兩個(gè)單元格，每個(gè)單元格代表高折射率區(qū)域和低折射率區(qū)域。腳本計(jì)算給定溫度范圍內(nèi)的所有S參數(shù)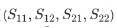
。但在這里，我們將主要關(guān)注光柵的反射
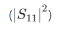，如下所示。觀察到峰值反射（對(duì)應(yīng)于布拉格波長(zhǎng)）約為90%，并且隨著溫度從25℃升高到1.000℃，呈現(xiàn)紅移。
[1] Damien Kinet, Patrice Mégret, Keith W. Goossen, Liang Qiu, Dirk Heider and Christophe Caucheteur, “Fiber Bragg Grating Sensors toward Structural Health Monitoring in Composite Materials: Challenges and Solutions”,Sensors 2014, 14, 7394-7419, doi:10.3390/s140407394
[2] Wenyuan Wang, Yongqin Yu, Youfu Geng, and Xuejin Li 'Measurements of thermo-optic coefficient of standard single mode fiber in large temperature range', Proc. SPIE 9620, 2015 International Conference on Optical Instruments and Technology: Optical Sensors and Applications, 96200Y (10 August 2015); https://doi.org/10.1117/12.2193091
.Hill and G. Meltz, 'Fiber Bragg grating technology fundamentals and overview,' in Journal of Lightwave Technology, vol. 15, no. 8, pp. 1263-1276, Aug. 1997, doi: 10.1109/50.618320.
[3] Hsieh TS, Chen YC, Chiang CC. “Analysis and Optimization of Thermodiffusion of an FBG Sensor in the Gas Nitriding Process.” Micromachines (Basel). 2016 Dec 12;7(12):227. doi: 10.3390/mi7120227. PMID: 30404399; PMCID: PMC6190027.
[4] Du Yanliang, Li Jianzhi, Liu Chenxi, “A Novel Fiber Bragg Grating Temperature Compensated Strain Sensor”, 2008 First International Conference on Intelligent Networks and Intelligent Systems, DOI 10.1109/ICINIS.2008.27
[5] “The Effect of Temperature and Pressure on the Refractive index of Some Oxide Glasses”, Roy M. Waxler, G.W.Cleek, Journal of Research of the National Bureau of Standards – A.Physics and Chemistry, Vol 77A, No.6, November-December 1973.