對于表面不規(guī)則度的公差分析是鏡頭設(shè)計過程中保證生產(chǎn)加工得到的實際光學(xué)元件能夠達(dá)到預(yù)期性能的重要環(huán)節(jié)?？赡芤鸸鈱W(xué)性能變化的因素包括但不限于光學(xué)表面的加工誤差、所用模具的加工誤差、注塑造成的不規(guī)則度、光學(xué)元件與傳感器間的校準(zhǔn)誤差、光學(xué)表面的粗糙度誤差以及厚度誤差。
將這些不規(guī)則度參數(shù)化將有利于公差分析，公差操作數(shù) TEZI 就是一個很好的例子。TEZI 操作數(shù)使用 Zernike 多項式來表示不規(guī)則度，一些低頻表面誤差可以用該參數(shù)化公式來評價公差。并且非常高頻的表面誤差將引起光束產(chǎn)生大角度散射，光學(xué)系統(tǒng)中可以將這部分作為能量損耗忽略不計。然而，介于這兩者之間的中頻表面誤差，參數(shù)化建模就存在一些難度，不僅在于難以使用多項式進(jìn)行表示，而且在于不能作為系統(tǒng)損耗而忽略。
本文我們以以金剛石車削為例，解釋為什么需要一個中頻誤差的分析模型。我們定義了一個表達(dá)式來建模這種不規(guī)則度，并在示例中使用點列圖和公差分析進(jìn)行展示。結(jié)尾處，說明使用這種模型時應(yīng)注意的限制條件。
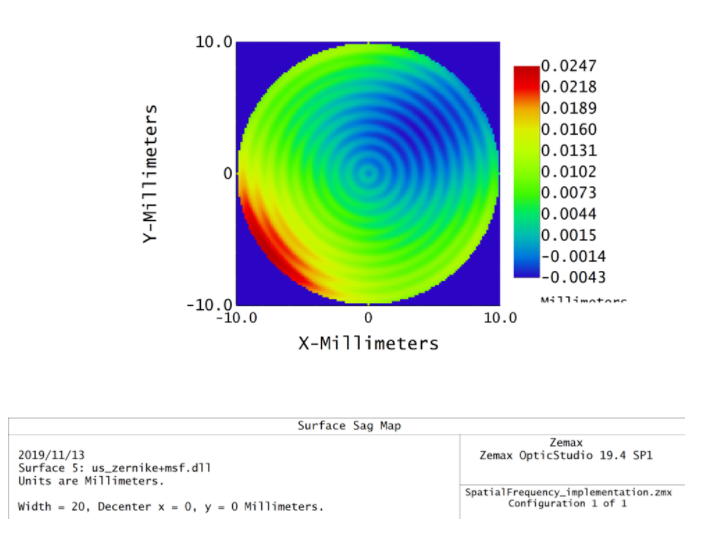
在光學(xué)表面制造時，通常用表面不規(guī)則度或RMS誤差的形式來衡量一個表面與一個完美標(biāo)準(zhǔn)表面之間的差異。例如，在632.8 nm的He-Ne激光測試下，一個成品透鏡或反射鏡的表面不規(guī)則度大概為0.1λRMS。再以定制透鏡為例，如零位檢驗中使用的透鏡，表面不規(guī)則度大概為0.01 λRMS。
空間頻率分為不同的頻域：
如果空間頻率高，類似于表面粗糙度，我們可以將其考慮為光學(xué)系統(tǒng)的損耗
如果空間頻率低，對于低頻部分我們可以用如?Zernike?多項式等方法表示其形狀變化
當(dāng)空間頻率高至無法使用多項式輕松定義（孔徑中包含10個周期以上[2]）或空間頻率低至其造成的影響不能忽略時（相對于波長的波紋周期大于從給定的表面到像面光路的1/10[2,3]），我們統(tǒng)稱為中頻部分。
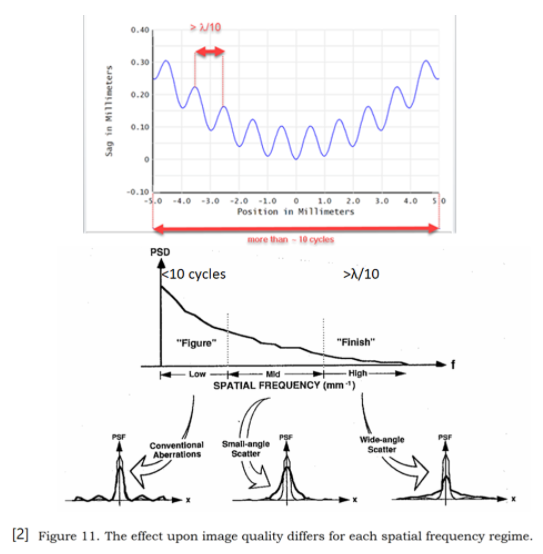
這些中頻誤差可能導(dǎo)致系統(tǒng)分辨率降低、產(chǎn)生雜散光、降低照明系統(tǒng)均勻性等。因此在繪制圖紙或訂購零件之前，這些誤差應(yīng)體現(xiàn)在光學(xué)元件公差分析中。如果是專門定制的零件，與制造商結(jié)合空間頻率詳細(xì)討論表面不規(guī)則度形式是至關(guān)重要的，制造商可能會提供類似零件的性能數(shù)據(jù)或者提供一個較接近的不規(guī)則度結(jié)果預(yù)測。
通常情況下，不規(guī)則度的形式是未知的。如果是常規(guī)拋光，那么假定不規(guī)則度會引起低階像差（如光焦度和像散）比較保險，并可以在OpticStudio中使用多種不同方法模擬這種不規(guī)則度。然而，與傳統(tǒng)的表面加工不同，金剛石車削可以作為一個特別的案列，需要預(yù)測零件中的中頻至高頻旋轉(zhuǎn)對稱波紋。
金剛石車削是以金剛石為切削工具的車削方法，廣泛應(yīng)用于從晶體、金屬、丙烯酸等材料的高質(zhì)量非球面光學(xué)元件加工中，塑料光學(xué)元件也通常使用金剛石車削加工得到的模具來注塑成型。它是一種用鑲金剛石刀頭的旋轉(zhuǎn)車刀對精密元件進(jìn)行機(jī)械加工的過程，根據(jù)加工工藝的不同可以產(chǎn)生從P-V深度為0.1微米的中高頻誤差或幾個微米的低頻誤差。常見相關(guān)術(shù)語為“單點金剛石車削 (SPDT) ”。金剛石車削可以獲得高的反射亮度，因此不需要額外的拋光或拋光。然而，金剛石刀頭的軌跡會在零件局部留下一定頻率的波紋。
在OpticStudio或光學(xué)系統(tǒng)中，有多種方法可能用于表達(dá)不規(guī)則度：
Zernike?項模擬表面不規(guī)則度
網(wǎng)格數(shù)據(jù)表示表面不規(guī)則度
利用擴(kuò)展多項式或切比雪夫多項式得到的三維誤差對加工表面的輪廓數(shù)據(jù)進(jìn)行擬合
擴(kuò)展奇次非球面可以擬合旋轉(zhuǎn)對稱測量數(shù)據(jù)
多項式的參數(shù)擬合在高頻上往往表現(xiàn)不佳，因為表面上波紋的數(shù)量取決于參數(shù)方程中多項式的數(shù)量。隨著高頻誤差的增加，僅依靠多項式擬合可能會變得不準(zhǔn)確。此外，當(dāng)使用過多多項式或者網(wǎng)格矢高點時，將不存在一個像蒙特卡羅那樣的實用公差統(tǒng)計分析方法來分析它們可能包含的各種不規(guī)則度。
我們可以從加工過程中預(yù)測金剛石車削引起的中頻旋轉(zhuǎn)對稱不規(guī)則度[3]。本文我們提出一種將多個表面組合起來，以形成一個用戶自定義表面的方法，來完成諸如公差分析這類需要改變參數(shù)的任務(wù)。
表達(dá)式如下所示：
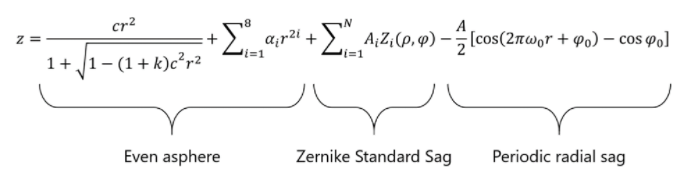
上述表達(dá)式包含三個部分，從左至右分別是：偶次非球面部分，Zernike部分，周期矢高部分。其中，Zernike部分與?Zernike Standard矢高面型完全相同，使用的是?Zernike?多項式。Zernike?多項式為單位圓環(huán)上一系列正交的多項式。周期性部分是以一個固定振幅和頻率疊加到表面上的矢高值，其形式與OpticStudio?內(nèi)置的“us_eaperiodic.dll”?相同。中頻表達(dá)式可以看做是?Zernike Standard?矢高疊加上一個周期性變化的一種變體，其中：
z?是表面矢高
r?是以透鏡單位為單位的極坐標(biāo)矢徑長度
c?是曲率
k?是圓錐系數(shù)
αi?第i個非球面的稀疏
N?是?Zernike?系數(shù)的個數(shù)
Ai?第?i?個?Zernike Standard?多項式的系數(shù)
ρ?是光線歸一化徑向坐標(biāo)
φ?是光線角向坐標(biāo)
A?是周期項振幅
ω0?是周期項頻率（單位是長度單位的倒數(shù)）
φ0?是相位偏移，如鏡頭數(shù)據(jù)編輯器中采用角度制輸入，但是計算時轉(zhuǎn)換為弧度制
為了描述中頻表面的建模應(yīng)用，我們將使用附件中的'SpatialFrequency_implementation.zar'文件作為示例，或者也可以提取其中的“us zernike+msf.dll“文件，并將其保存在{Zemax}\documents\Zemax\DLL\Surfaces中的文檔文件夾中。
讓我們來查看中頻表面的設(shè)置：首先，像其他所有面型一樣，我們需要打開表面屬性，將表面類型改為用戶自定義，并選擇 “us\u zernike+msf.dll'。
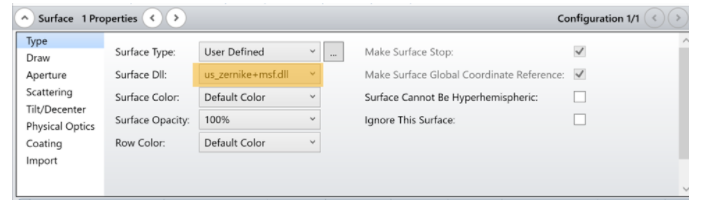
DLL加載到表面上后，我們就可以看到我們所需的參數(shù)。如下圖所示，非球面項以16階結(jié)束，然后是周期性徑向矢高的三個參數(shù) A、w0、phi0。Zernike參數(shù)疊加周期性矢高，就完成了用戶定義表面的定義。
由于我們的用戶定義曲面“us_zernike+msf.dll”是從Zernike Standard 矢高面型和另一個用戶定義曲面“us_eaperiodic.dll”派生的，因此我們可以先研究一下它們，再比較一下我們的新面型有什么不同。
首先，讓我們比較一下'us_eaperiodic.dll'和我們的中頻面 'us_zernike+msf.dll'，讓二者使用相同的設(shè)置，具體采用：
振幅 A = 0.01mm
頻率 w0 =1 cycle/mm
相位 φ0 = 0.01 degrees
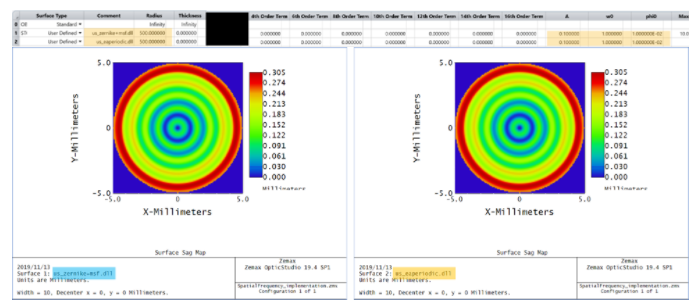
我們看到，左側(cè)的中頻曲面“us_zernike+msf.dll”（以藍(lán)色突出顯示），右側(cè)的周期曲面“us_eaperiodic.dll”（以橙色突出顯示）具有相同的曲面矢高輪廓。
同樣，讓我們對比一下 Zernike Standard 矢高曲面和我們的中頻面“us_Zernike+msf.dll”有何異同。我們將使兩個曲面在其設(shè)置中完全相同，并檢查與 Zernike 項的一致性。具體設(shè)置為：
振幅 A = 0.01mm
頻率 w0 =1 cycle/mm
相位 φ0 = 0.01 degrees
Zernike X 偏心 = 0.2
Zernike Y 偏心 = -0.1
Zernike 1 = 1.00E-003
Zernike 2 = -4.00E-003
Zernike 3 = -2.00E-003
Zernike 4 = 1.00E-003
Zernike 5 = 5.00E-004
Zernike 6 = 1.00E-004
Zernike 7 = 2.00E-003
Zernike 8 = 1.00E-003
Zernike 9 = -5.00E-003
?Zernike 10 = 1.00E-003
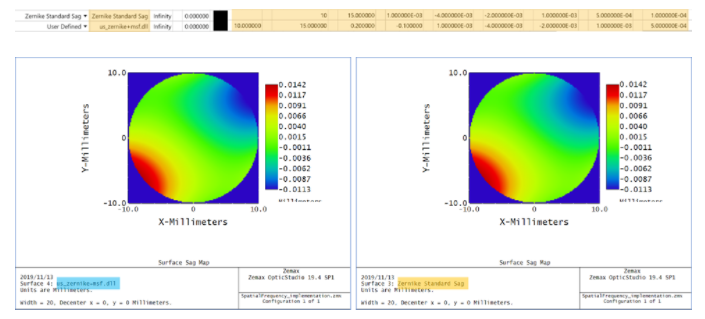
我們看到，左側(cè)的中頻曲面“us_zernike+msf.dll”（以藍(lán)色突出顯示）和右側(cè)的 Zernike Standard 矢高曲面（以橙色突出顯示）具有相同的曲面矢高輪廓。
所以，我們可以放心大膽地假設(shè)：中頻曲面同時具有周期曲面和Zernike多項式的性質(zhì)，當(dāng)然還有標(biāo)準(zhǔn)的非球面輪廓。下面顯示了具有Zernike多項式不規(guī)則度和周期性波紋狀不規(guī)則度的曲面的示例，以供說明。
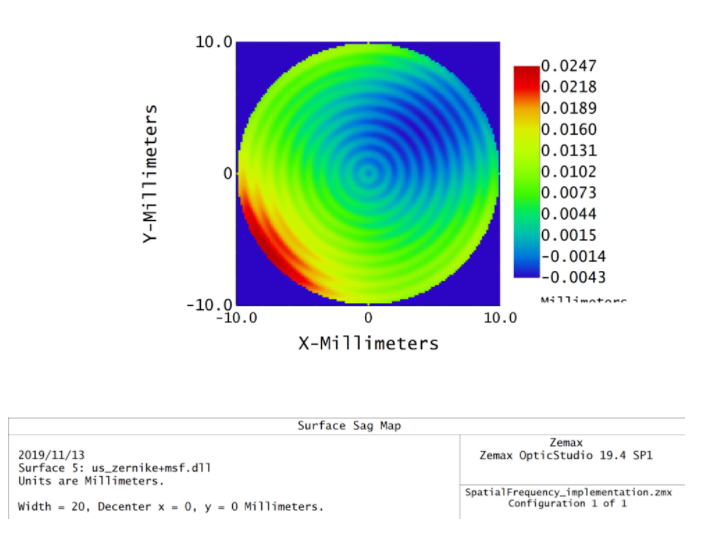
編寫和編譯DLL等內(nèi)容不在本文的討論范圍之內(nèi)，但您可以參閱 “如何編寫用戶自定義DLL”文章獲取更多信息。
https://support.zemax.com/hc/zh-cn/articles/1500005577602
本文使用的DLL已在附件中提供。
簡單周期面“us_eaperiodic.dll”及其源代碼可以在文件夾{Zemax}\Documents\Zemax\DLL\Surfaces中找到，這是OpticsStudio安裝時就自帶的表面。
此示例用于觀察中頻曲面的點列圖，我們將使用本文附件中的“spatial frequency_spot diagrams.zar”文件。
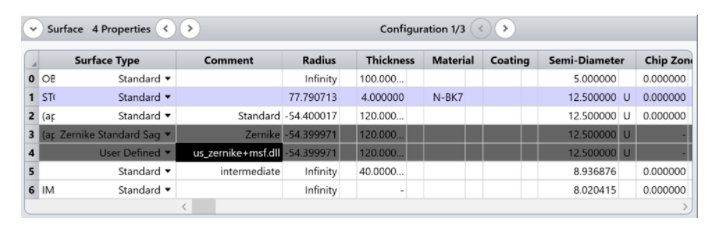
設(shè)計目標(biāo)為物高 5mm，物距 100mm，后焦 160mm的非球面透鏡，分別采用三個表面：
1.一個標(biāo)準(zhǔn)面
2.一個 Zernike Standard 矢高面
3.使用 'us_zernike+msf.dll' 建立的中頻面。其中Zernike Standard 矢高面和中頻面參數(shù)相同，具體為：
振幅 = 5.00E-004mm
頻率 w0 =1 cycle/mm
相位 φ0 = 0.00 degrees
Zernike X 偏心 = 0.2
Zernike Y 偏心= -0.1
Zernike 1 = 1.00E-003
Zernike 2 = -4.00E-003
Zernike 3 = -2.00E-003
Zernike 4 = 1.00E-003
Zernike 5 = 5.00E-004
Zernike 6 = 1.00E-004
Zernike 7 = 2.00E-003
Zernike 8 = 1.00E-003
Zernike 9 = -5.00E-003
Zernike 10 = 1.00E-003
從光線出射端測試，為了方便觀測，中頻面放在距離像面40 mm的位置：
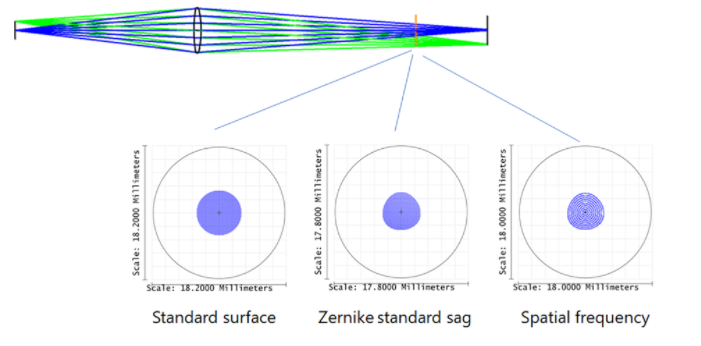
我們可以看到非常經(jīng)典的旋轉(zhuǎn)對稱的標(biāo)準(zhǔn)面光斑輪廓。Zernike Standard 矢高面由于Zernike多項式項的存在，顯示出輕微變形的光斑輪廓。中頻曲面具有相同的Zernike多項式參數(shù)，此外還有周期參數(shù)，表現(xiàn)為光斑中的圓環(huán)。
在像面，我們用下面的結(jié)構(gòu)矩陣點列圖 (Configuration Matrix Spot Diagram) 來說明這一點。結(jié)構(gòu)1為標(biāo)準(zhǔn)面，結(jié)構(gòu)2為 Zernike Standard 矢高面，結(jié)構(gòu)3為中頻曲面。
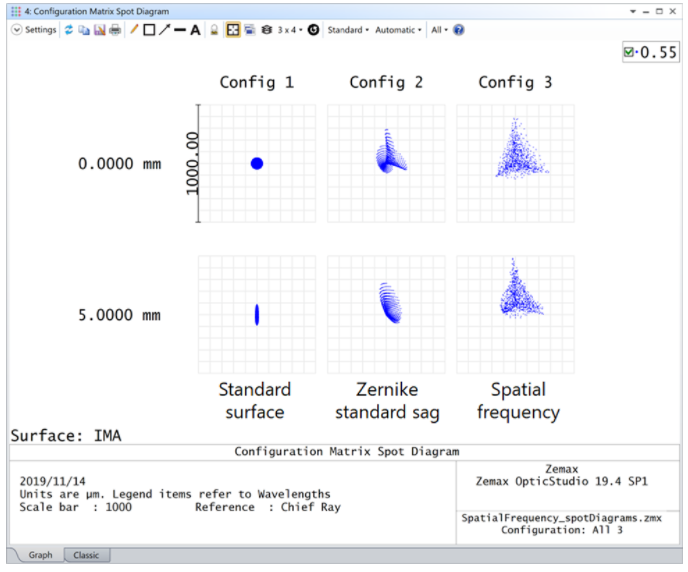
標(biāo)準(zhǔn)表面沒有不規(guī)則度，它也將作為我們的參考標(biāo)準(zhǔn)。Zernike Standard 矢高面稍微有些變形。中頻曲面大體上與 Zernike Standard 矢高面相同，但由于曲面上形成的波紋形狀，產(chǎn)生了相對于 Zernike 光斑輪廓不同的周圍散射光線。我們可以預(yù)期這樣的鏡頭制造時會有部分鏡頭會因光線改變了預(yù)定路徑而不符合設(shè)計的表面規(guī)定。
此示例用于觀察天塞物鏡中頻表面的公差，我們將使用文章附件中的“spacealfrequency_tol.zar”文件。
我們使用的是Paul Rudolph (USP721240)[4] 的經(jīng)典天塞鏡頭設(shè)計，系統(tǒng)的第 一個表面上為中空間頻率表面（橙色突出顯示）。
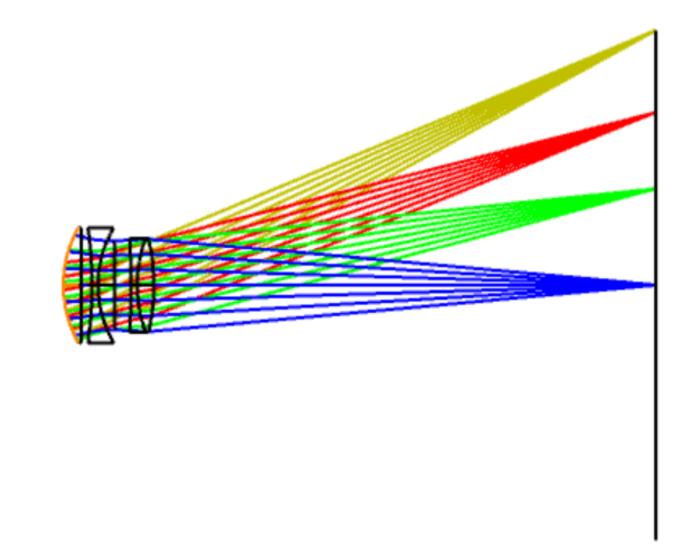
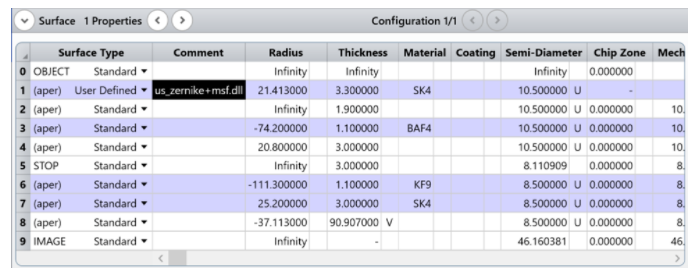
以下圖所示的參數(shù)設(shè)置公差向?qū)в糜诠罘治觯?/span>
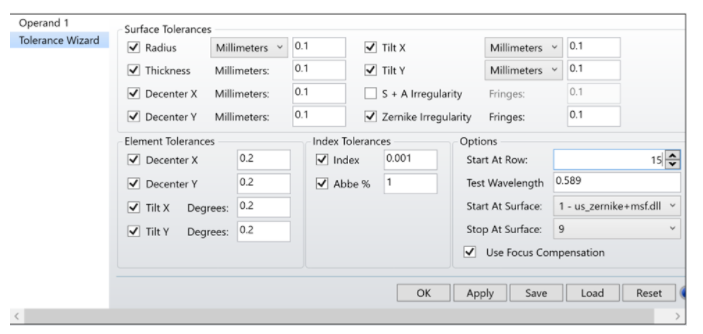
在OpticStudio中，TEZI公差操作數(shù)允許對具有軸上孔徑的標(biāo)準(zhǔn)面、非球面或環(huán)形面表面的不規(guī)則性進(jìn)行自動公差擾動，其他表面類型則不允許使用?TEZI。但我們可以仍使用?TPAR?來擾動曲面的參數(shù)，多邊形物體和CAD文件（如STEP和IGES文件）則無法進(jìn)行擾動。
設(shè)置參數(shù)為：
振幅= 5.00E-004mm
頻率?w0?=1 cycle/mm
相位?φ0?= 0.00 degrees
Zernike X?偏心?= 0.2
Zernike Y?偏心?= -0.1
Zernike 1 = 1.00E-003
Zernike 2 = -4.00E-003
Zernike 3 = -2.00E-003
Zernike 4 = 1.00E-003
Zernike 5 = 5.00E-004
Zernike 6 = 1.00E-004
Zernike 7 = 2.00E-003
Zernike 8 = 1.00E-003
Zernike 9 = -5.00E-003
Zernike 10 = 1.00E-003
這些參數(shù)表示Zernike?項在整個表面上具有約?5?微米的?RMS?誤差，周期項振幅約為?0.5?微米，周期為?1?周期/毫米，或者說在整個表面有?20?個周期。
在進(jìn)行公差分析之前，我們需要對公差參數(shù)進(jìn)行一些調(diào)整。首先，由于我們的用戶定義的中頻“us_zernike+msf.dll”曲面不是TEZI支持的曲面類型之一，所以必須刪除曲面1的操作數(shù)，并將其替換為TPAR。
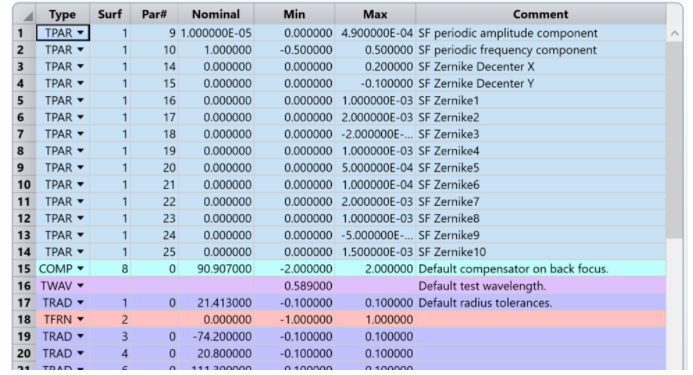
舉例來說，TPAR(1,9)指表面1的第9個參數(shù)（振幅擾動）。同理，TPAR(1,10)表示表面1的第10個參數(shù)（周期擾動）。TPAR(1,16)到TPAR(1,25)是中頻曲面的Zernike項，如編輯器中所示，名義值為零或非常小，并且隨著蒙特卡羅分析的每次迭代而增加。
靈敏度分析表明，上述TPAR(1,9)是影響極嚴(yán)重的因素之一，說明表面波紋狀不規(guī)則度的幅度越大，系統(tǒng)的性能下降越大。我們還可以看到基于平方根和的均方根光斑半徑預(yù)估值。
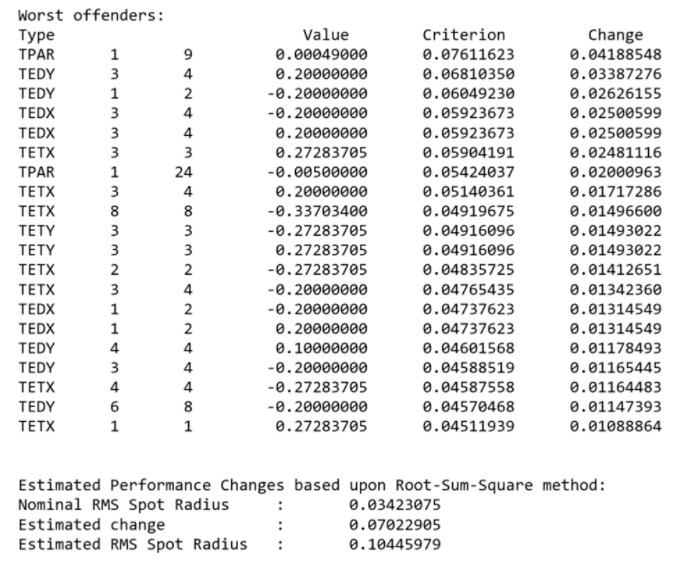
以RMS光斑半徑為標(biāo)準(zhǔn)，優(yōu)化后焦長度，蒙特卡羅循環(huán)1000次。
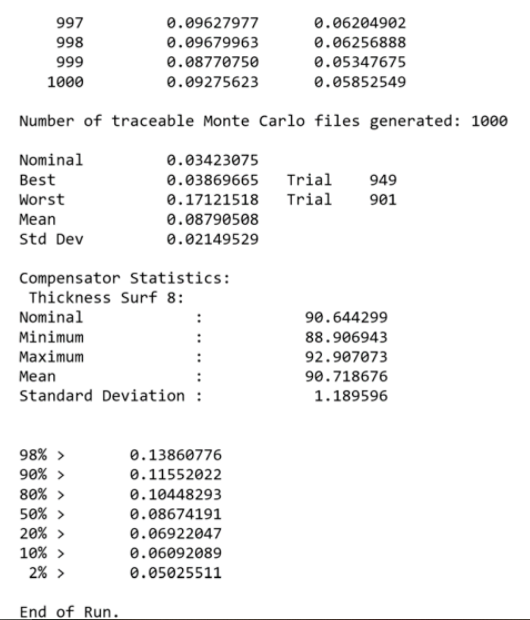
附件中提供的“MC_BEST.ZMX”和“MC_WORST.ZMX”可以用來檢查。
我們可能會碰到獲得性能較差結(jié)果的情況。所以，這要求我們的公差參數(shù)必須設(shè)置為合理的值，或者憑借經(jīng)驗得出的更好的參數(shù)方案。制造商也可能提供類似零件的性能表現(xiàn)信息，或者幫助預(yù)測比較壞的結(jié)果，在確定設(shè)計方案前，這些信息是鏡頭設(shè)計過程中的關(guān)鍵。
參考資料
[1] Diamond turning an acrylic dome (YouTube)
[2] J. E. Harvey and A. Thompson, Proc. SPIE 2576
[3] R. N. Youngworth and B. D. Stone, Applied Optics 39(13)
[4] Paul Rudolph - USP721240
相關(guān)閱讀
使用OpticStudio進(jìn)行閃光激光雷達(dá)系統(tǒng)建模（下）
使用OpticStudio進(jìn)行閃光激光雷達(dá)系統(tǒng)建模（中）
使用OpticStudio進(jìn)行閃光激光雷達(dá)系統(tǒng)建模（上）
大功率激光系統(tǒng)的STOP分析5：OpticStudio STAR模塊工作流程
大功率激光系統(tǒng)的STOP分析4: 使用OpticStudio仿真激光吸收
大功率激光系統(tǒng)的STOP分析3：使用OpticsBuilder完成光機(jī)初始設(shè)計
大功率激光系統(tǒng)的STOP分析2：如何進(jìn)行光機(jī)械設(shè)計準(zhǔn)備
大功率激光系統(tǒng)的STOP分析1：如何使用OpticStudio優(yōu)化光學(xué)設(shè)置